rev :: [t] -> [t] rev [] = [] rev (a:x) = rev x ++ [a]
Source code: reverse.hs.
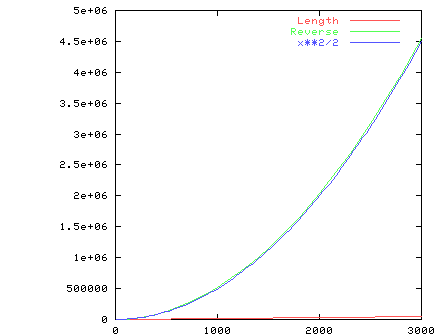
The program was loaded into Hugs and run with lists of length between 10 and 3000. The number of reductions required for computing the length of the lists was compared with the number of reductions for computing the length of the reversed lists. The number of reductions for computing the length of a list is seen to be linear wheras the number of reductions for computing the length of the reversed list is quadratic. The reason that rev requires a quadratic number of reductions is because list catenation requires a number of reductions that is proportional to the length of the first list.

Note: The function reverse contained in the prelude of Hugs only requires a linear number of reductions. Another implementation only requiring a linear number of reductions is reverse2.hs.
| n | Reductions | |
|---|---|---|
| length [1..n] | length (rev [1..n]) | |
| 10 | 189 | 246 |
| 100 | 1620 | 6771 |
| 200 | 3220 | 23521 |
| 300 | 4820 | 50271 |
| 400 | 6420 | 87021 |
| 500 | 8020 | 133771 |
| 600 | 9620 | 190521 |
| 700 | 11220 | 257271 |
| 800 | 12820 | 334021 |
| 900 | 14420 | 420771 |
| 1000 | 16020 | 517521 |
| 1100 | 17620 | 624271 |
| 1200 | 19220 | 741021 |
| 1300 | 20820 | 867771 |
| 1400 | 22420 | 1004521 |
| 1500 | 24020 | 1151271 |
| 1600 | 25620 | 1308021 |
| 1700 | 27220 | 1474771 |
| 1800 | 28820 | 1651521 |
| 1900 | 30420 | 1838271 |
| 2000 | 32020 | 2035030 |
| 2100 | 33620 | 2241771 |
| 2200 | 35220 | 2458521 |
| 2300 | 36820 | 2685271 |
| 2400 | 38420 | 2922021 |
| 2500 | 40020 | 3168771 |
| 2600 | 41620 | 3425521 |
| 2700 | 43220 | 3692271 |
| 2800 | 44820 | 3969021 |
| 2900 | 46420 | 4255771 |
| 3000 | 48020 | 4552521 |