Klip de udleverede ark (card.pdf | card.ps) ud langs de tynde linier. Derved fås en stak kort med tilfældige numre. Kortene kan blandes ved at rode dem rundt på bordet og samle dem i en stak bagefter - dette skal gøres før hver brug af kortene i de følgende øvelse (hvad der ikke vil blive nævnt igen).
Opgaven er nu at sortere kortene (til stigende orden, d.v.s. mindste kort øverst).
Overvej kort, hvordan I vil gøre, og afprøv så metoden (lad gerne flere prøve samtidigt).
Spørgsmål:
Beskriv metoden I brugte detaljeret nok til at andre kan udføre den (5-10 liniers svar).
Find en nabogruppe, og udveksel jeres beskrivelse fra øvelse 1 med hinanden. Lad to eller tre forskellige personer i jeres gruppe udføre nabogruppens metode (gerne samtidigt, så flest muligt laver noget). Tag tid for alle, og find gennemsnittet.
Spørgsmål:
Angiv gennemsnittet.
Følgende algoritme kaldes SelectionSort:
Lad U være den usorterede stak af kort, og lad S være en stak af kort, som til at starte med er tom. Gentag følgende til U er tom:Find det mindste kort i U, og sæt det bagerst i S.
Øv først lidt for at blive sikker i algoritmen. Lad to eller tre personer køre algoritmen, tag tid undervejs, og udregn gennemsnittet af tiderne.
Spørgsmål:
Angiv gennemsnittet.
Følgende algoritme kaldes InsertionSort:
Lad U være den usorterede stak af kort, og lad S være en stak af kort, som til at starte med er tom. Gentag følgende til U er tom:Tag øverste kort i U og indsæt det på rette plads i S, d.v.s. på en position så alle kort før det er mindre, og alle efter det er større.
Øv først lidt for at blive sikker i algoritmen. Lad derefter to eller tre personer køre algoritmen, tag tid undervejs, og udregn gennemsnittet af tiderne.
Spørgsmål:
Angiv gennemsnittet.
Beskriv metoden i bruger til at finde den "rette plads i S" detaljeret nok til at andre kan udføre den (5-10 liniers svar).
Følgende algoritme kaldes MergeSort:
Lad U være den usorterede stak af kort. Lav U om til mange sorterede stakke af størrelse 2 ved gentagne gange at tage to kort fra U, lægge det mindste øverst, og lægge de to kort til side i en bunke for sig.To bunker kan nu flettes til een ny bunke ved at kigge på det øverste kort i de to bunker og flytte det mindste af de to over som det bagerste i den nye bunke (og det gentages til de to bunker er tomme).
En runde i algoritmen består i at flette de nuværende bunker sammen to og to, til bunker af dobbelt størrelse.
De nye bunker bruges i næste runde. Algoritmen består i at lave sådanne runder, til man står med kun een bunke i alt.
Øv først lidt for at blive sikker i algoritmen. Lad to eller tre personer køre algoritmen, tag tid undervejs, og udregn gennemsnittet af tiderne.
Spørgsmål:
Angiv gennemsnittet.
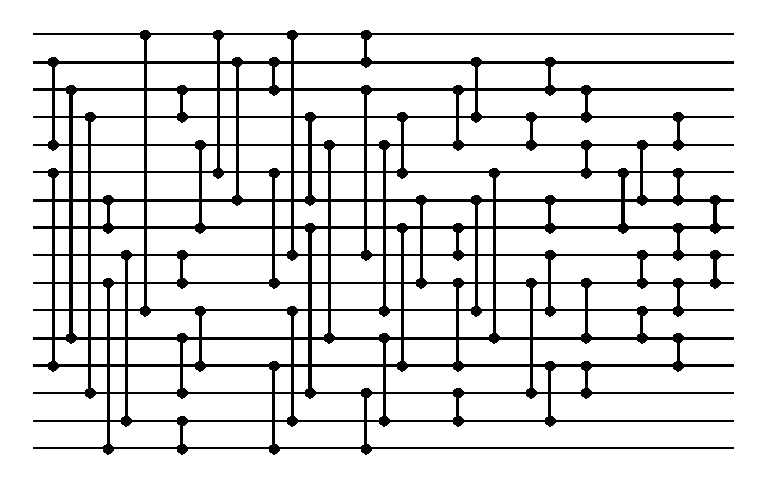
For at et sorterningsnetværk faktisk sorter input kræves det at ligegyldt hvilken rækkefølge elementerne kommer ind til venstre, så kommer disse ud i sorteret rækkefølge til højre,
Nedenstående er et sorteringsnetværk for 16 elementer der bruger 60
sammenligninger.

Læs introduktion til sorteringsnetværk som også beskriver en applet til brug for opgaven.
Følgende er links til en Java applet der tillader at man designer sorteringsnetværk for hhv:
Appleten kan checke om et tegnet netværk faktisk sorterer alle mulige input.Spørgsmål:
Hvad er de mindste sorteringsnetværk I kan finde for at sortere henholdsvis 4, 8, og 10 elementer? (Husk at uploade jeres netværk fra Java appleten)
Følgende algoritme kaldes RadixSort:
Algoritmen kører i runder, een runde for hvert ciffer som er i de tal, der skal sorteres.I første runde fordeles kortene fra den usorterede stak U i ti bunker efter hvilket ciffer der står sidst i tallet (på "ener-pladsen").
De ti bunker lægges oven i hinanden til een bunke, således at 9'er-bunken ligger under 8'er-bunken, som ligger under 7'er-bunken, og så videre. Man slutter med 0'er-bunken, som skal ligge øverst.
I anden runde fordeles kortene fra denne ene bunke igen i ti bunker, men denne gang efter hvilket ciffer der står næstsidst i tallet (på "tier-pladsen"). Man skal fordele kortene i bunken nedefra og opefter (d.v.s. nederste kort lægges først ud).
I tredie runde fordeles kortene fra denne ene bunke igen i ti bunker, men denne gang efter hvilket ciffer der står trediesidst i tallet (på "hundrede-pladsen"). Man skal igen fordele kortene i bunken nedefra og opefter (d.v.s. nederste kort lægges først ud).
Hvis der var flere cifre i tallene, skulle man blot forsætte med flere runder.
Øv først lidt for at blive sikker i algoritmen. Lad to eller tre personer køre algoritmen, tag tid undervejs, og udregn gennemsnittet af tiderne.
Spørgsmål:
Angiv gennemsnittet.
Vi vil i denne øvelse prøve at vurdere, hvor lang tid algoritmerne generelt bruger på at sortere.
Det er klart at det tager længere tid at sortere, jo flere kort, der er. Hvis N står for antallet af kort, bør vores vurdering altså afhænge af N.
Men for samme N kan man godt tænke sig at den tid en algoritme bruger, afhænger af hvilken orden kortene starter i. F.eks. vil en algoritme, som starter med at kontrollere om kortene ER sorteret, være hurtig hvis dette rent faktisk er tilfældet.
Vi kan derfor forsøge at sige noget om, hvad den bedst mulige og værst mulige tid er, som funktion af N.
Lad os for nemheds skyld sige at det alt i alt tager eet sekund at kigge på et kort, sammenligne det med at andet kort og evt. flytte kortet et andet sted hen.
Under denne antaglse, angiv matematiske udtryk (indeholdende N) som I mener angiver det mindste og største antal sekunder, algoritmen bruger.
Angiv også to rækkefølger af tallene 1,2,3,4,5 (d.v.s. N = 5) som giver mindste og største køretid for sortering af disse tal. Hvis mindste og største køretid er det samme (d.v.s. alle rækkefølger tager lige lang tid), skrives dette i stedet for rækkefølgerne.
Spørgsmål:
Udfyld nedenstående to tabeller:
---------- Tabel 1 ----------
ALGORITME BEDSTE TID V&Aelig;RSTE TID
SelectionSort
InsertionSort
MergeSort
RadixSort
---------- Tabel 2 ----------
ALGORITME BEDSTE R&Aelig;KKEFØLGE V&Aelig;RSTE R&Aelig;KKEFØLGE
SelectionSort
InsertionSort
MergeSort
RadixSort
I denne øvelse betragter vi algoritmer som sorterer elementer ved kun at sammenligne elementer (som f.eks. InsertionSort, SelectionSort og MergeSort, men ikke RadixSort da RadixSort kigger på de enkelte cifre i tallene).
For enhver sorterings-algoritme findes der et værste input, hvor algoritmen skal foretage mange sammenligninger. Nedenstående tabel angiver det værste antal sammenligniner der skal til for at sortere input op til 12 elementer. F.eks. findes der en algoritme der for input bestående af 7 elementer aldrig bruger mere end 13 sammenligninger for at sortere elementerne, og ydermere kan man bevise at ingen algoritme kan sortere alle input bestående af 7 elementer med 12 eller fære sammenligninger.
Antal elementer : 1 2 3 4 5 6 7 8 9 10 11 12 Optimale antal sammenligninger : 0 1 _ _ 7 10 13 16 19 22 26 30I denne opgave ønskes de to manglende værdier for input bestående af 3 henholdsvis 4 elementer fundet. For hvert af de to inputstørrelser forsøg
Spørgsmål:
Hvad er det optimale antal sammenligninger for at sortere 3 og 4 elementer ?
Kan I anvende samarbejde mellem flere personer til at bringe tidsforbruget i sorteringsalgoritmerne ned?
Målet er at f.eks. fire personer kan blive færdige med arbejdet på ca. en fjerdedel af tiden for een person.
Overvej for algoritmerne Mergesort og SelectionSort hvorledes fire personer kan samarbejde således at algoritmen bliver udført på ca. en fjerdedel af tiden for een person.
Spørgsmål:
Hvorledes kan fire personer samarbejde således at algoritmen bliver udført på ca. en fjerdedel af tiden for een person (10-25 liniers svar i alt):
Mergesort:
SelectionSort:
Følgende er links til en Java applet der tillader at man designer hash-funktioner for tre forskellige mængder:
Spørgsmål:
Angiv for de tre input mængder en hash-funktion der spreder bedst muligt ud, dvs. en hash-funktion hvor tabel indgangen med de fleste elementer har færrest mulige elementer. (Husk at uploade jeres hash-funktion fra Java appleten)
Betragt følgende liste af tal.
30 83 73 80 59 63 41 78 68 82 53 31 22 74 6 36 99 57 43 60
Øvelsen er at slette så få af disse tal som muligt, så de resterende tal står i voksende orden. Hvis for eksempel alt på nær de første to tal slettes, har man en voksende følge tilbage af længde 2. Ved at slette alt på nær det første, tredie, ottende og tiende opnår man det samme, men har slettet færre tal og har en voksende følge tilbage af længde 4.
Spørgsmål:
Hvor lang er den længste voksende følge man kan opnå ?
I denne opgave betragter vi to strenge hver bestående af en sekvens af bogstaverne A, C, G og T. I denne øvelse søges den længste delsekvens der forekommer i begge strenge. F.eks. angiver *-makeringerne at sekvensen AGCGATGA er en delsekvens i begge strenge, men det er nemt at se at der findes længere fælles delsekvenser.
ACTAGGTAACTTGAGTTTAGGCACGTTAGCTA
* * * * * * * *
GATTCAGGTAGTACGATCAGTAGCTAGTCTGA
* * *** ***
Spørgsmål:
Angiv en længst mulig delsekvens som forekommer i begge strenge i ovenstående eksempel.
Sammen med arrayet ønsker vi at gemme en begrænset antal yderligere delsummer, således at det værste antal sammenligninger for delsum(i,j) spørgsmål altid kan beregnes hurtigere. F.eks. ved at gemme delsummen af den midterste 1/3 af elementerne (I[N/3]+....+I[2N/3-1], kan man besvare alle delsum(i,j) med højest 2/3*N additioner. Intuitivt så falder det værste antal additioner for delsum(i,j) spørgsmål med antallet af delsummer der er gemt.
Det antages at der kun må anvendes additioner på elementer (d.v.s. det er f.eks. ikke er tilladte at anvende minus).
Læs introduktion til delsum problemet som også beskriver en applet til brug for opgaven.
Spørgsmål:
Hvad er det mindste antal delsummer I behøver at gemme for et array af længde 16, således at alle delsum(i,j) spørgsmål kan besvares med henholdvis 1 og 2 additioner?
Brug appleten til at designe jeres mængde af delsummer og til at checke om alle delsum(i,j) spørgsmål kræver højest 1 og 2 additioner. Uploade jeres resultat til high score listen.
Nedenstående viser en graf med knuder A,B,C,...,W og hvor nogle knuder er forbundet med kanter.
En sti er en sekvens af knuder hvor der er kanter imellem efterfølgende par af knuder i sekvensen, f.eks. er S,A,L,N en sti i nedenstående graf da der findes kanter mellem følgende par af knuder: (S,A), (A,L) og (L,N).
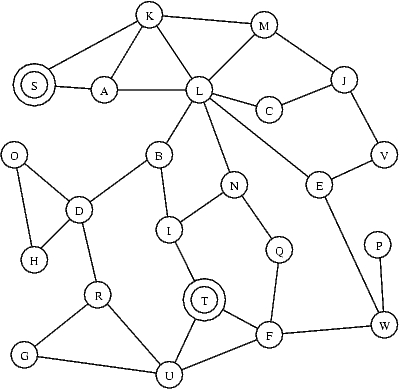
Spørgsmål:
Angiv en sti fra S til T i ovenstående graf som besøger flest mulige knuder, men hvor hver knude besøges højst een gang på stien.
I denne øvelse betragter vi grafer med vægte på kanterne.
Længden af en sti er summen af vægtene af kanterne langs stien. F.eks. har stien S,A,D,R,T vægt 27 = 4+10+5+8.

Spørgsmål:
Angiv længden af den kortest vej fra S til T i ovenstående graf.
I denne øvelse skal der vælges en person fra gruppen til at hente et ark med puslespil (puzzle.pdf | puzzle.ps) fra instruktoren. Arket indeholder tre puslespil, som alle handler om at samle polygoner til et kvadrat. Der er tre puslespil, med 2, 4 og 8 brikker.
Uden at vise de andre arket (da løsningen i så fald bliver kendt), klipper personen brikkerne ud.
Tre andre personer løser derefter hvert sit puslespil (vend brikkerne om, så eventuelle rester af streger ikke kan bruges som hjælp).
Tag tid på løsningen (stop løsningen af det store puslespil efter 5 minutter, hvis man ikke har løst det inden da).
Spørgsmål:
Angiv tiden for det tre løsninger.
2 brikker:
4 brikker:
8 brikker:
Vælg en sorteringsalgoritme (gerne jeres egen). Sorter bunker med 8, 16 og 32 (alle) kort, og tag tid herfor.
Spørgsmål:
Angiv tiden for det tre sorteringer:
8 kort:
16 kort:
32 kort:
To simple matematikopgaver.
De må gerne besvares ved afprøvning på lommeregner eller ved plot af funktioner på grafisk lommeregner.
Spørgsmål:
Fra og med hvilket N er 0.01*N^2 større 100*N ?
Fra og med hvilket N er 0.0001*2^N større 10000*N ?
Endnu en matematikopgave.
Vi ser her på to computere, X og Y. Den gamle computer X kan lave 1.000.000 beregninger per sekund, mens den helt nye model Y kan lave 1.000.000.000 beregninger per sekund.
For forskellige køretider for algoritmer ønsker vi nu at beregne hvor store input der kan behandles inden for en givet tidsfrist.
Udfyld nedenstående tabel med største værdi af inputstørrelsen N, der kan behandles inden for det angivne tidsrum og på den angivne computer, når køretiden for algoritmen, udtrykt ved størrelsen N af input, er som angivet.
Spørgsmål:
Udfyld følgende tabel:
---------- Tabel ----------
KØRETID X I ET SEKUND X I ET ÅR Y I ET SEKUND Y I ET ÅR
N
N*log(N)
N^2
100*N^2
N^3
2^N