Ugesedlen anfører til hver uge hvilke forelæsninger der planlægges holdt i nærmeste fremtid. De anførte øvelsesopgaver bliver gennemgået til TØ i den pågældende uge. De vil typisk behandle stof fra den foregående uge. Den obligatoriske afleveringsopgave skal regnes og afleveres i grupper af 1-3 personer i udgangen af den pågældende uge, typisk i weekenden, efter aftale med holdets instruktor. Afleveringsopgaven på ugesedlen til uge x afleveres mellem øvelserne i uge x og x+1. Så har man nemlig gavn af gennemgangen af relateret stof til TØ i uge x til at regne afleveringsopgaven. Instruktoren vil gennemgå opgaven til TØ i uge x+1 og tilbagelevere den rettede aflevering.
[Brodal] opgaver 1-3.
Opgaverne 1-7 nedenfor forudsætter ingen algoritmiske kundskaber. De præsenterer relativt simple opgaver for konkrete data. Læserens opgave er at finde svaret ved håndkraft. Opgavernes hovedformål er at illustrere problemet i at håndtere et stort antal tilfælde. Sagt på en anden måde, er hensigten at skabe frustration ved anvendelsen af ligefremme metoder. Alle opgaverne er taget fra Udi Manber: "Introduction to Algorithms - A Creative Approach", Addison-Wesley, 1989.
Betragt følgende liste af tal.
9 44 32 12 7 42 34 92 35 37 41 8 20 27 83 64 61 28 39 93 29 17 13 14 55 21 66 72 23 73 99 1 2 88 77 3 65 83 84 62 5 11 74 68 76 78 67 75 69 70 22
Din opgave er at slette så få af disse tal som muligt, så de resterende tal står i voksende orden. Hvis du for eksempel sletter alt på nær de første to tal, har du en voksende følge tilbage. Ved at slette alt på nær det første, tredje, sjette og ottende tal opnår du det samme, men har slettet færre tal.
Input er en liste af heltal som forneden. Betydningen af parret (x,y) er, at x venter på et svar fra y. Når x venter, kan den ikke gøre andet; den kan specielt ikke svare på spørsmål fra andre, der måtte vente på den. Problemet er at finde en følge af par (x1,x2), (x2,x3),... (x(k-1),xk), (xk, x1) for et eller andet k. Hvis et sådant k findes, går systemet i baglås. Ingen i følgen kan fortsætte, da alle venter på hinanden.
Du har lov til at bruge papir og blyant og må gennenføre vilkårlige beregninger (fx sammenligne tal, opstille tabeller). Men du har ikke lov til at tegne en figur. (Du har dog lov til at tegne figurer, der ikke har med det konkrete input at gøre, for at finde en generel løsning til den slags problemer).
(1,16), (2,21), (2,25), (2,22), (23,50), (23,47), (24,1), (25,10), (35,7), (36,45), (36,37), (38,42), (39,41), (12,37), (12,23), (12,3), (12,20), (14,25), (41,9), (42,3), (43,5), (43,22), (29,2), (30,48), (31,15), (32,17), (6,45), (6,1), (5,35), (5,20), (5,28), (5,11), (48,4), (48,10), (49,32), (7,31), (7,4), (5,33), (6,29), (6,12), (6,11), (6,3), (6,17), (45,27), (47,34), (48,20), (7,40), (7,34), (8,11), (9,19), (11,30), (11,4), (11,22), (11,25), (20,24), (21,23), (21,46), (22,47), (23,49), (3,39), (3,34), (4,14), (4,37), (5,42), (5,8), (15,2), (15,50), (15,4), (15,37), (16,13), (17,38), (18,28), (19,8), (26,15), (26,42), (27,18), (28,35), (13,36), (13,50), (13,34), (13,22), (29,34), (29,38), (29,30), (29,16), (44,33), (44,36), (44,7), (44,3), (44,32), (44,21), (33,9), (33,21), (33,35), (33,19), (33,41), (26,10), (26,44), (26,16), (26,39), (26,17)
Input der denne 15 gange 15-tabel:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 3 | - | 1 | 9 | 6 | 2 | 1 | 7 | 4 | 2 | 8 | 3 | - |
| 2 | 7 | 0 | 2 | - | - | - | - | 2 | 1 | 6 | 9 | 1 | 7 | 2 | 8 |
| 3 | 8 | - | 0 | 8 | 9 | 3 | 6 | 8 | 5 | 8 | - | 8 | - | 3 | - |
| 4 | - | 8 | - | 0 | - | 5 | 4 | - | - | 1 | 1 | 9 | - | 8 | - |
| 5 | 9 | - | 8 | - | 0 | 3 | 2 | 7 | 5 | 8 | - | 1 | - | 4 | 2 |
| 6 | 3 | 2 | - | 3 | 6 | 0 | 5 | 3 | 2 | - | 8 | 7 | 2 | - | 8 |
| 7 | 2 | - | - | 2 | 8 | - | 0 | 6 | 2 | - | 8 | 8 | 2 | - | 4 |
| 8 | 1 | 1 | - | - | 2 | 3 | 8 | 0 | - | 1 | 1 | - | 2 | 7 | - |
| 9 | 4 | - | 9 | - | 2 | 9 | - | 2 | 0 | 4 | 9 | 3 | - | - | - |
| 10 | - | - | - | - | 1 | 8 | - | 7 | 1 | 0 | 3 | - | - | - | 2 |
| 11 | 3 | 8 | 7 | 1 | - | - | 3 | 8 | - | - | 0 | 2 | 9 | 2 | 1 |
| 12 | 3 | - | 1 | 2 | 8 | 1 | 1 | - | 5 | 1 | 9 | 0 | 2 | - | 9 |
| 13 | 7 | - | 3 | 1 | 6 | - | - | 2 | - | 3 | - | 9 | 0 | 2 | - |
| 14 | 2 | 9 | 6 | - | 7 | - | 9 | - | 3 | - | 1 | 1 | 9 | 0 | - |
| 15 | 2 | 9 | 2 | 1 | - | - | 1 | - | 4 | 3 | 6 | 5 | 1 | - | 0 |
Den i'te række og den i'te søjle (for vilkårligt i) repræsenterer samme sted. Hver indgang i tabellen indikerer den direkte afstand mellem stederne: indgangen i den i'te række og j'te søjle angiver den direkte afstand fra i til j. En streg indikerer, at der ikke er nogen direkte forbindelse mellem de pågældende steder. Den direkte afstand behøver ikke at være den korteste afstand; der kan være en kortere vej mellem to steder via et tredje sted (eller flere steder). For eksempel går den korteste vej fra 1 til 6 gennem 5 og 12.
Find den korteste vej mellem
Betragt igen tabellen fra sidste opgave. Find de korteste veje mellem 5 og alle andre steder.
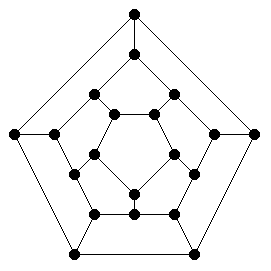
Betragt følgende graf:

Find en lukket vej (altså en, der kommer tilbage til udgangspunktet) langs kanterne i grafen, som passerer hver knude præcis én gang.
Denne graf repræsenterer kanterne i et dodekaeder (det regulære polyeder med tolv sider). Den irske matematiker Sir William R. Hamilton var den første til at betrage dette problem og har siden lagt navn til sådanne, Hamiltonske, veje.
Det følgende er et labyrintproblem, selvom labyrinten er givet i form af tal (og ikke et billede). Labyrinten er indeholdt i et rektangel med 11 rækker og søjler, nummereret fra 0 til 10. Man bevæger sig i labyrinten langs rækkerne og søjlerne - op, ned, højre, venstre. Start er (0,0) og mål er (10,10). Følgende punkter angiver forhindringer, som man ikke kan betræde:
(3,2) (6,6) (7,0) (2,8) (5,9) (8,4) (2,4) (0,8) (1,3) (6,3) (9,3) (1,9) (3,0) (3,7) (4,2) (7,8) (2,2) (4,5) (5,6) (10,5) (6,2) (6,10) (4,0) (7,5) (7,9) (8,1) (5,7) (4,4) (8,7) (9,2) (10,9) (2,6)
Find en vej fra start til mål, som ikke indeholder nogen forhindringer. Find derpå den korteste vej.
Følgende liste angiver antallet af valgmandsstemmer for hver amerikansk stat til præsidentvalget i 1988 (den kandidat, der har flertallet af stemmer i en stat, får alle valgmandens stemmer fra den stat).
| Alabama | 9 | Alaska | 3 | Arizona | 7 |
| Arkansas | 6 | Californien | 47 | Colorado | 8 |
| Connecticut | 8 | Delaware | 3 | Florida | 21 |
| Georgia | 12 | Hawaii | 4 | Idaho | 4 |
| Illinois | 24 | Indiana | 12 | Iowa | 8 |
| Kansas | 7 | Kentucky | 9 | Lousiana | 10 |
| Maine | 4 | Maryland | 10 | Massachusetts | 13 |
| Michigan | 20 | Minnesota | 10 | Mississippi | 7 |
| Missouri | 11 | Montana | 4 | Nebraska | 5 |
| Nevada | 4 | New Hampshire | 4 | New Jersey | 16 |
| New Mexico | 5 | New York | 36 | North Carolina | 13 |
| North Dakota | 3 | Ohio | 23 | Oklahoma | 8 |
| Oregon | 7 | Pennsylvania | 25 | Rhode Island | 4 |
| South Carolina | 8 | South Dakota | 3 | Tennessee | 11 |
| Texas | 29 | Utah | 5 | Vermont | 3 |
| Virginia | 12 | Washington | 10 | Washington, D.C. | 3 |
| West Virginia | 6 | Wisconsin | 11 | Wyoming | 3 |
Der er 538 stemmer. Find ud at, om det er (matematisk) muligt, at valget ender uafgjort. (Dette er et eksempel på et opdelingsproblem og et specialtilfælde af rygsæksproblemet).
Betragt det maksimale delsumsproblem i 2 dimensioner (jfr. [Bentley] opgave 8.7.13).