Obligatorisk opgave i dADS, forår 2003

Den obligatoriske opgave går ud på at skrive et Java-program, der kan finde en størst mulig pardannelse i en ikke-orienteret, todelt graf. Opgaven er struktureret som tre delopgaver, der stilles i forbindelse med ugesedlerne for uge 16/17, 18 og 19. Ved besvarelse af opgaven er det tilladt at arbejde i grupper på indtil to personer. Man kan aflevere besvarelser af delopgaverne til sin instruktor ganske som var de almindelige afleveringsopgaver. Der vil ikke blive stillet andre afleveringsopgaver til de uger, hvor der er obligatorisk opgave på programmet.

De tre delopgaver lægger op til en skridtvis konstruktion af et Java-program, der realiserer en algoritme, der kan finde en størst mulig pardannelse. Selve forløbet kommer til at bestå af tre skridt: Først konstrueres en abstrakt algoritme, som bevises korrekt; dernæst designes der effektive datastrukturer; og til sidst foretages der en implementation i Java.

Det færdige program vil skulle demonstreres på data, der er hentet fra et skema-hold-planlægningsproblem fra det virkelige liv, samt på tilfældigt genererede data.

Den samlede besvarelse af opgaven (som består af besvarelser af tre delopgaver) skal afleveres på Datalogisk Informationskontor senest d. 12. maj 2003 kl. 12.00. Der er ingen mulighed for genaflevering. Besvarelsen skal være forsynet med den officielle forside i udfyldt stand og skal være samlet i plastomslag eller lignende.

Parringer, dækninger og parringsgrafer

En ikke-orienteret graf G=(V,E) er todelt, hvis knudemængden V kan deles i to disjunkte delmængder V₁ og V₂, således at alle kanterne i E forbinder en knude i V₁ med en knude i V₂.

En parring er en delmængde P af kanterne i E, hvor alle kanterne i P er knudedisjunkte.

En dækning er en delmængde D af knuderne i V, således at alle kanterne i E er incidente med mindst een knude fra D.

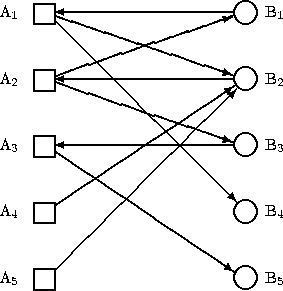
Nedenstående graf er et eksempel på en todelt graf. De fede kanter angiver parringen P = {{A₁, B₁}, {A₂, B₂}, {A₃, B₃}} af størrelse 3. Et eksempel på en dækning er knuderne D = {A₁, A₂, A₃, B₂}.

For en vilkårlig parring P og dækning D gælder der, at enhver kant i P er dækket af en knude i D, hvilket giver os følgende simple observation:

|P| |D|.

For en givet todelt graf G og parring P definerer vi den tilhørende parringsgraf til at være en orienteret graf G'=(V, E'), hvor kanterne i E' nu er orienterede. Kanter, der indgår i parringen P, er orienteret fra V₂ til V₁ og de øvrige kanter er orienteret fra V₁ til V₂. Knuder i V₁ lader vi være firkantede og knuder i V₂ runde.

For ovenstående graf og parring har vi følgende parringsgraf:

Firkantede knuder med indgrad 0 kaldes initialknuder, runde knuder med udgrad 0 kaldes terminalknuder. En vej fra en initialknude til en terminalknude kaldes en skiftevej.

Det er nemt at indse, at hvis der findes en skiftevej i en parringsgraf, så kan man, ved at ændre orienteringen på alle kanterne på skiftevejen, opnå en parring der er een større.

I ovenstående graf udgør (A₄, B₂, A₂, B₃, A₃, B₅) en skiftevej, og hvis vi ændrer orienteringen langs denne vej, så for vi følgende parringsgraf, der repræsenterer en parring, der er een større.

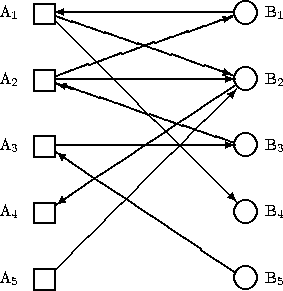
Den obligatoriske opgave går ud på at bruge denne teknik til at finde størst-mulig parring. Bemærk at den sidst opnåede parring i ovenstående graf indeholder 4 kanter, og at den derfor er størst mulig idet der også findes en dækning i grafen bestående af 4 knuder.

Opgave O1

Denne opgave går ud på at konstruere en algoritme til at finde størst mulig pardannelse.

Betragt følgende transitionssystem, der farver knuder i parringsgrafer. Ufarvede knuder kaldes hvide, skraverede knuder grå, og udfyldte knuder er sorte. De farvede grafer kaldes brogede.

Transitionssystem: Farvning af parringsgrafer
Konfigurationer:	Brogede parringsgrafer
Transitioner:				hvis indgraden af er 0
				hvis udgraden af er 0
				hvis udgraden af er 0

Lad nu P være en parring i en graf G og G' den tilhørende parringsgraf. I en slutkonfiguration for en proces, der starter med den hvide graf G', gælder der følgende:

U₁:Alle grå og sorte knuder kan nås fra en firkantet sort knude.

U₂: |P| = (antal ) + (antal ) i G'

U₃: Knudemængden bestående af , og dækker alle kanter i G.

1. Bevis U₁ vha. et passende invariansargument.
2. Bevis U₂ vha. et passende invariansargument.
3. Bevis U₃ ved at vise, at når ingen af transitionsreglerne kan anvendes, findes der ingen kanter af formen eller eller eller .
4. Betragt nu følgende abstrakte algoritme:

   Algorithm StørstMuligPardannelse(G):
   Input:	En ikke-orienteret, todelt graf G
   Output:	P, en størst mulig parring i G
   Method:	Lad G' være en parringsgraf for G
   	Farv G' v.hj.a. transitionssystemet ovenfor
   	// Invariant:U1 U2 U3
   	while    der findes en vej i G'   do
   	Opdatér G' mht.
   	Farv alle knuder i G' hvide
   	Farv G' v.hj.a. transitionssystemet ovenfor
   	Sæt P til mængden af ``venstreorienterede'' kanter i G'

   Argumentér for, at invarianten er gyldig og at algoritmen er korrekt.

5. Bevis følgende sætning, som viser, at der kan opstå lighedstegn i uligheden |P| |D| fra introduktionen.

   Sætning (König 1931). I enhver todelt graf er størrelsen af den maksimale parring lig størrelsen af den minimale dækning.