Computational Geometry (Fall 2008)

Project 3

(A) Lower envelope of half rays

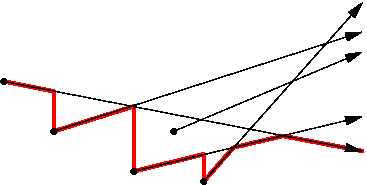
Consider n rightward rays in the plane. Describe an algorithm with running time 0(nlog n) for finding the lower envelope of the n rightward rays (shown in red in the example below). Your answer should include an argument about that the number of points/segments on the lower envelope is 0(n).

(B) Minimal points in R³

Consider n points p₁,p₂,...,p_n in R³. A point p_i = (x_i,y_i,z_i) is minimal if no other point p_j = (x_j,y_j,z_j) satisfies simultaniously x_j ≤ x_i, y_j ≤ y_i, and z_j ≤ z_i. Describe an algorithm that finds all minimal points in time 0(nlog^c n), where c is a small constant. In the example below the green points show the minimal points for a point set in R².

(C) Smallest enclosing rectangle

Describe an algorithm that given n points in the plane finds a rectangle of minimal area that contains all points. The rectangle is allowed to have sides that are not axis parallel (but the four corners should of course each be 90°). The running time of the algorithm should be 0(nlog n).

(D) Most Densely Polulated Unit Circle

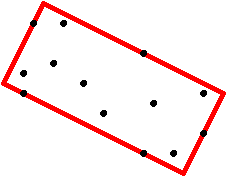
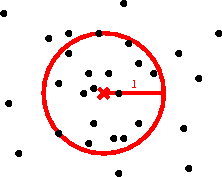
Describe an algorithm that given n points in the plane finds a circle of radius one containing the most numer of points. The algorithm should ideally have a running time of 0(n²).

Deadline: Monday January 12, 2009.

Important note: The project should be done in groups of up to three persons. The evaluation of the report will be part of the final grade.