The following exercises assumes no prior knowledge about algorithms, data structures or coding. They represent relatively simple problems on concrete data. Your task is to solve the exercises by hand. The main purpose of the exercises is to demonstrate how difficult it can be to solve large scale problems in a straight-forward an ad-hoc manner. Said differently, it illustrates why we need algorithms (i.e. mechanical procedures) that can be executed by a computer. All exercises are taken from Udi Manber: "Introduction to Algorithms - A Creative Approach", Addison-Wesley, 1989.
Note: Contrary to all later exercises, you are NOT expected to have solved these exercises before attending the first exercise session. However, having read through them is a good idea.
Consider the following list of numbers:
9 44 32 12 7 42 34 92 35 37 41 8 20 27 83 64 61 28 39 93 29 17 13 14 55 21 66 72 23 73 99 1 2 88 77 3 65 83 84 62 5 11 74 68 76 78 67 75 69 70 22
Your task is to delete as few of these numbers as possible, such that the remaining sequence of numbers is in ascending order (gets larger and larger from left to right). As an example, consider deleting all but the first two numbers. Then the remaining sequence 9, 44 is in ascending order. You could also delete everything, except the first, third, sixth and eights number to achieve the same (the sequence becomes 9, 32, 42, 92), but this time deleting even fewer numbers.
The following is a labyrinth problem, even though the labyrinth is presented in the form of numbers (and not an image). The labyrinth is contained in a rectangle with 11 rows and columns, numbered from 0 to 10. You move in the labyrinth along the rows and columns - up, down, right, left. The start is (0,0) and the goal is to get to (10,10). The following points represent obstacles that one cannot move into:
(3,2) (6,6) (7,0) (2,8) (5,9) (8,4) (2,4) (0,8) (1,3) (6,3) (9,3) (1,9) (3,0) (3,7) (4,2) (7,8) (2,2) (4,5) (5,6) (10,5) (6,2) (6,10) (4,0) (7,5) (7,9) (8,1) (5,7) (4,4) (8,7) (9,2) (10,9) (2,6)
Find a path from the start to the goal which does not contain any obstacles. Then find the shortest such path.
The input is a list of integers as below. The meaning of the pair (x,y) is that x is waiting for a reply from y. When x is waiting, it cannot do anything else; in particular, it cannot answer questions from others that might be waiting for it. The problem is to find a sequence of pairs (x1,x2), (x2, x3), ... , (xk-1,xk), (xk,x1) for some k. If such a k exists, then the system deadlocks. No one in the sequence can continue, as they are all waiting for each other.
You are allowed to use paper and a pencil and may perform arbitrary computations (e.g. like comparing numbers, creating tables). But you are not allowed to draw a figure. (You are allowed to draw figures that doesn't relate to the concrete input, in order to find a general solution to this kind of problem).
(1,16), (2,21), (2,25), (2,22), (23,50), (23,47), (24,1), (25,10), (35,7), (36,45), (36,37), (38,42), (39,41), (12,37), (12,23), (12,3), (12,20), (14,25), (41,9), (42,3), (43,5), (43,22), (29,2), (30,48), (31,15), (32,17), (6,45), (6,1), (5,35), (5,20), (5,28), (5,11), (48,4), (48,10), (49,32), (7,31), (7,4), (5,33), (6,29), (6,12), (6,11), (6,3), (6,17), (45,27), (47,34), (48,20), (7,40), (7,34), (8,11), (9,19), (11,30), (11,4), (11,22), (11,25), (20,24), (21,23), (21,46), (22,47), (23,49), (3,39), (3,34), (4,14), (4,37), (5,42), (5,8), (15,2), (15,50), (15,4), (15,37), (16,13), (17,38), (18,28), (19,8), (26,15), (26,42), (27,18), (28,35), (13,36), (13,50), (13,34), (13,22), (29,34), (29,38), (29,30), (29,16), (44,33), (44,36), (44,7), (44,3), (44,32), (44,21), (33,9), (33,21), (33,35), (33,19), (33,41), (26,10), (26,44), (26,16), (26,39), (26,17)
The input is the following 15 by 15 table:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 3 | - | 1 | 9 | 6 | 2 | 1 | 7 | 4 | 2 | 8 | 3 | - |
| 2 | 7 | 0 | 2 | - | - | - | - | 2 | 1 | 6 | 9 | 1 | 7 | 2 | 8 |
| 3 | 8 | - | 0 | 8 | 9 | 3 | 6 | 8 | 5 | 8 | - | 8 | - | 3 | - |
| 4 | - | 8 | - | 0 | - | 5 | 4 | - | - | 1 | 1 | 9 | - | 8 | - |
| 5 | 9 | - | 8 | - | 0 | 3 | 2 | 7 | 5 | 8 | - | 1 | - | 4 | 2 |
| 6 | 3 | 2 | - | 3 | 6 | 0 | 5 | 3 | 2 | - | 8 | 7 | 2 | - | 8 |
| 7 | 2 | - | - | 2 | 8 | - | 0 | 6 | 2 | - | 8 | 8 | 2 | - | 4 |
| 8 | 1 | 1 | - | - | 2 | 3 | 8 | 0 | - | 1 | 1 | - | 2 | 7 | - |
| 9 | 4 | - | 9 | - | 2 | 9 | - | 2 | 0 | 4 | 9 | 3 | - | - | - |
| 10 | - | - | - | - | 1 | 8 | - | 7 | 1 | 0 | 3 | - | - | - | 2 |
| 11 | 3 | 8 | 7 | 1 | - | - | 3 | 8 | - | - | 0 | 2 | 9 | 2 | 1 |
| 12 | 3 | - | 1 | 2 | 8 | 1 | 1 | - | 5 | 1 | 9 | 0 | 2 | - | 9 |
| 13 | 7 | - | 3 | 1 | 6 | - | - | 2 | - | 3 | - | 9 | 0 | 2 | - |
| 14 | 2 | 9 | 6 | - | 7 | - | 9 | - | 3 | - | 1 | 1 | 9 | 0 | - |
| 15 | 2 | 9 | 2 | 1 | - | - | 1 | - | 4 | 3 | 6 | 5 | 1 | - | 0 |
The i'th row and i'th column (for arbitrary i) represents the same location. Every entry of the table indicates the direct distance between the locations: the entry in the i'th row and j'th column indicates the direct distance from i to j. A dash - indicates that there is no direct connection between the two locations. The direct distance is not necessarily the shortest distance; there could be a shorter path between two locations via a third location (or more). For example, the shortest path from 1 to 6 is through 5 and 12.
Find the shortest path between
Consider the table from the previous exercise once again. Find the shortest path from 5 to all other locations.
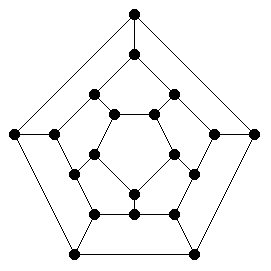
Consider the following graph:

Find a closed path (that is, a path that returns to its origin/start) along the edges of the graph, which visits every node exactly once.
The Irish mathematician Sir William R. Hamilton was the first to consider this problem and has laid name to such Hamiltonian path.
The following list gives the number of electoral votes for every American State at the presidential election in 2016 (the candidate with the most votes in a state receives all the electoral votes from that state).
| Alabama | 9 | Alaska | 3 | Arizona | 11 |
| Arkansas | 6 | California | 55 | Colorado | 9 |
| Connecticut | 7 | Delaware | 3 | Florida | 29 |
| Georgia | 16 | Hawaii | 4 | Idaho | 4 |
| Illinois | 20 | Indiana | 11 | Iowa | 6 |
| Kansas | 6 | Kentucky | 8 | Lousiana | 8 |
| Maine | 4 | Maryland | 10 | Massachusetts | 11 |
| Michigan | 16 | Minnesota | 10 | Mississippi | 6 |
| Missouri | 10 | Montana | 3 | Nebraska | 5 |
| Nevada | 6 | New Hampshire | 4 | New Jersey | 14 |
| New Mexico | 5 | New York | 29 | North Carolina | 15 |
| North Dakota | 3 | Ohio | 18 | Oklahoma | 7 |
| Oregon | 7 | Pennsylvania | 20 | Rhode Island | 4 |
| South Carolina | 9 | South Dakota | 3 | Tennessee | 11 |
| Texas | 38 | Utah | 6 | Vermont | 3 |
| Virginia | 13 | Washington | 12 | Washington D. C. | 3 |
| West Virginia | 5 | Wisconsin | 10 | Wyoming | 3 |
There are 538 electoral votes in total. Determine whether it is (mathematically) possible that the election ends in a tie (equally many electoral votes to the two candidates). (This is an example of a partitioning problem and a special case of the knapsack problem).